РАЗНОСТНАЯ СХЕМА КАБАРЕ

Одной из фундаментальных проблем вычислительной математики, актуальной с точки зрения реализации практических задач в сфере энергетики, является проблема «сеточного переноса». «Сеточный перенос» является критически важным элементом математического моделирования таких гидродинамических явлений, как турбулентные течения при больших числах Рейнольдса в элементах энергетических установок, когерентные вихревые структуры в атмосфере и океанах, генерация звука турбулентными струями в задачах аэроакустики.

Производительность современной вычислительной техники растет очень быстрыми темпами. Достижение петафлопсного уровня производительности суперкомпьютеров позволяет подойти к решению задач с критическим порогом точности, обусловленным многомасштабностью и мультифизичностью реальных процессов. Прежде всего, речь идет о процессах турбулентности, которые характеризуются наличием большого количества масштабов. Однако прежние методы расчетов и численные алгоритмы едва ли применимы для расчетов на современных суперкомпьютерах. Сегодня требуются совершенно новые подходы.

Одной из фундаментальных проблем пост-петафлопсной вычислительной математики является проблема сеточного переноса. Сеточный перенос — это ключевой элемент предсказательного математического моделирования таких гидродинамических явлений, как турбулентные течения при больших числах Рейнольдса в элементах энергетических установок, когерентные вихревые структуры в атмосфере и океанах, генерация звука турбулентными струями в задачах аэроакустики. Задача ставится следующим образом: имеется некая обобщенная система уравнений гидродинамики, точнее, система для обобщенной гидродинамики. В левой части стоит некий гиперболический оператор, в правой — эллиптический с малым параметром. Такая система описывает очень большое количество процессов, в числе которых уравнения Навье-Стокса, уравнения газовой динамики, магнитной гидродинамики, переноса нейтронных излучений и так далее. Гиперболичность левой части означает, что в течение некоторого периода времени до тех пор, пока характеристики одного семейства не пересекаются, решение является обратимым по времени. При разработке соответствующих численных алгоритмов требуется, чтобы обратимость сохранялась и на уровне этих алгоритмов.

Задачи с доминирующим сеточным переносом

В 1998 г. в ИБРАЭ РАН была разработана новая разностная схема для простейшего уравнения переноса, получившая наименование КАБАРЕ. В процессе доработки и ряда последовательных обобщений схемы появилась возможность ее применения к таким сложным задачам, как решение многомерных уравнений адвекции – диффузии с доминирующей адвекцией (сеточным переносом) и систем законов сохранения гиперболического типа, моделирование двумерных газодинамических течений в ортогональных координатах и двумерных несжимаемых течений, описываемых уравнениями Навье–Стокса в (P, u, v) и в (w, y), (w, u, v) переменных, обобщение на четырехугольные косоугольные сетки и неструктурированные гексагональные косоугольные сетки. Дальнейшие исследования направлены на изучение новых возможностей расчета экстремальных ударно-волновых течений и решения актуальных задач аэроакустики в применении к моделированию гидродинамических процессов в атомных реакторах.

Схема КАБАРЕ представляет собой новую высокоэффективную вычислительную технологию численного решения систем законов сохранения гиперболического типа с доминирующим сеточным переносом, и относится к вычислительным алгоритмам нового поколения, ориентированным на суперкомпьютеры экзафлопсного класса. 

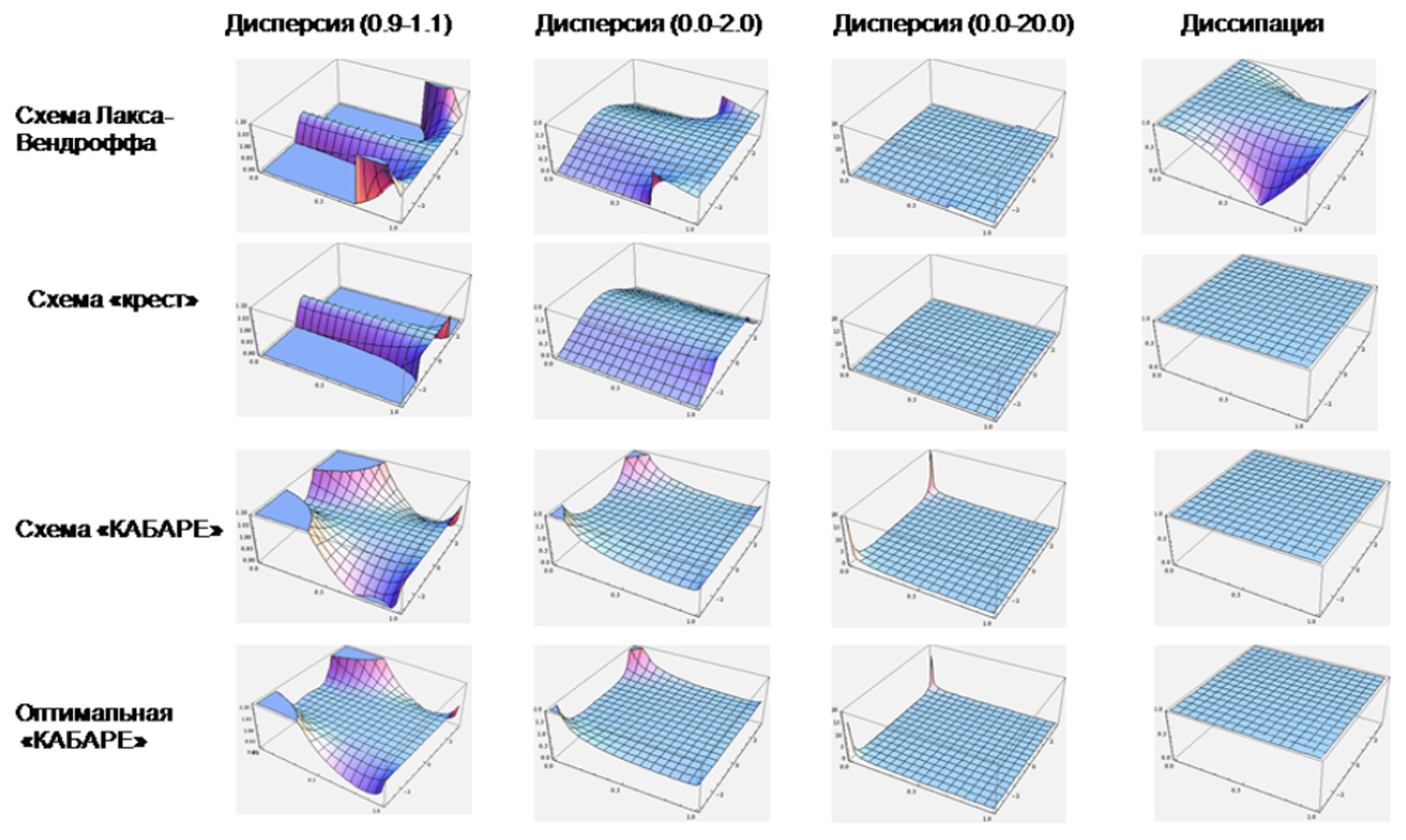
Эволюция дисперсионных свойств численных методов решения простейшего уравнения переноса

Cхема Лакса-Вендрофа характеризуется большой неравномерностью диссипативной и дисперсионной поверхностей. Более точная схема «крест» отличается малой диссипацией, но значительной дисперсией. В оптимизированной схеме КАБАРЕ диссипативные потери отсутствуют, а погрешности, обусловленные дисперсией, весьма малы практически на всем интервале волновых чисел, доступных на данной волновой сетке.

Схема КАБАРЕ обладает свойством временной обратимости. Благодаря этому амплитудные ошибки алгоритма отсутствуют, каждая из гармоник не затухает и не возрастает.

Следует отметить, что схема КАБАРЕ не приводит к существенному затуханию акустических возмущений (возмущений порядка P/P₀ = 10^–3 — 10^–6), характерному для других известных схем, в том числе и при наличии достаточно сложных пространственно–временных фоновых течений. Расчетным путем было установлено, что схема обеспечивает постоянство амплитуд двумерных вихрей с неподвижной осью, причем как для сжимаемой, так и для несжимаемой жидкости. По своему значению это свойство в вычислительной математике сравнимо с явлением сверхпроводимости в электротехнике. Это позволяет использовать схему КАБАРЕ в расчетах вихревых и турбулентных течений при больших числах Рейнольдса, как в приближении крупных вихрей без явного использования подсеточных моделей турбулентности (LES), так и в рамках прямого моделирования турбулентности при детальном разрешении колмогоровского масштаба (DNS – приближения) без каких либо настроечных параметров. 

Вычислительный шаблон схемы КАБАРЕ является предельно компактным, умещающимся в одну пространственно–временную расчетную ячейку. Это позволяет очень просто задавать граничные условия в сложных расчетных областях и обеспечивать максимальную вычислительную эффективность распараллеливания при проведении масштабных параллельных вычислений на многопроцессорных вычислительных комплексах.

а)   б) 

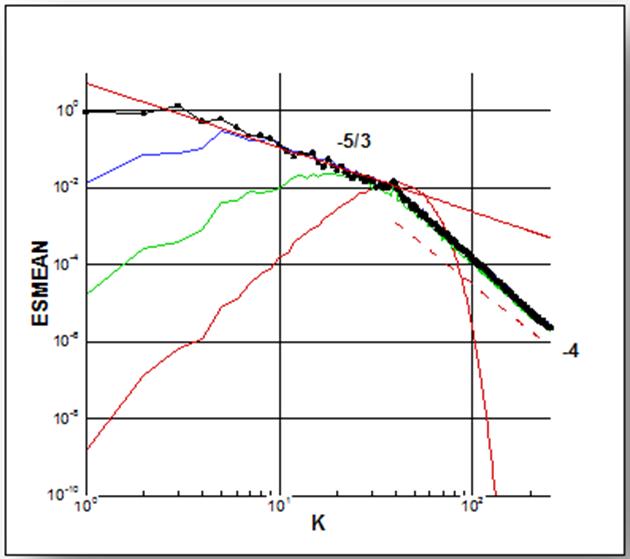
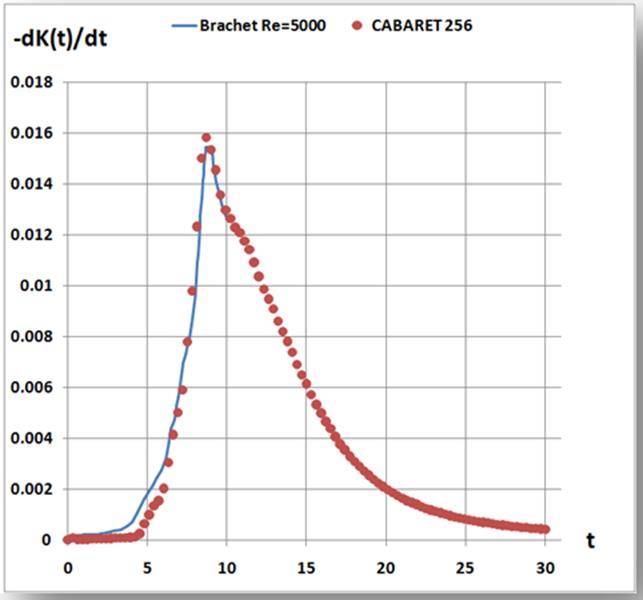
Прямое численное моделирование затухания однородной изотропной турбулентности.
а) двумерный спектр с форсингом («–5/3» + «–4»);  б) скорость диссипации, сравнение с DNS.

Распределение скорости потока при больших числах Рейнольдса во фрагменте теплообменника со свинцово-висмутовым теплоносителем в проектируемом реакторе СВБР-100

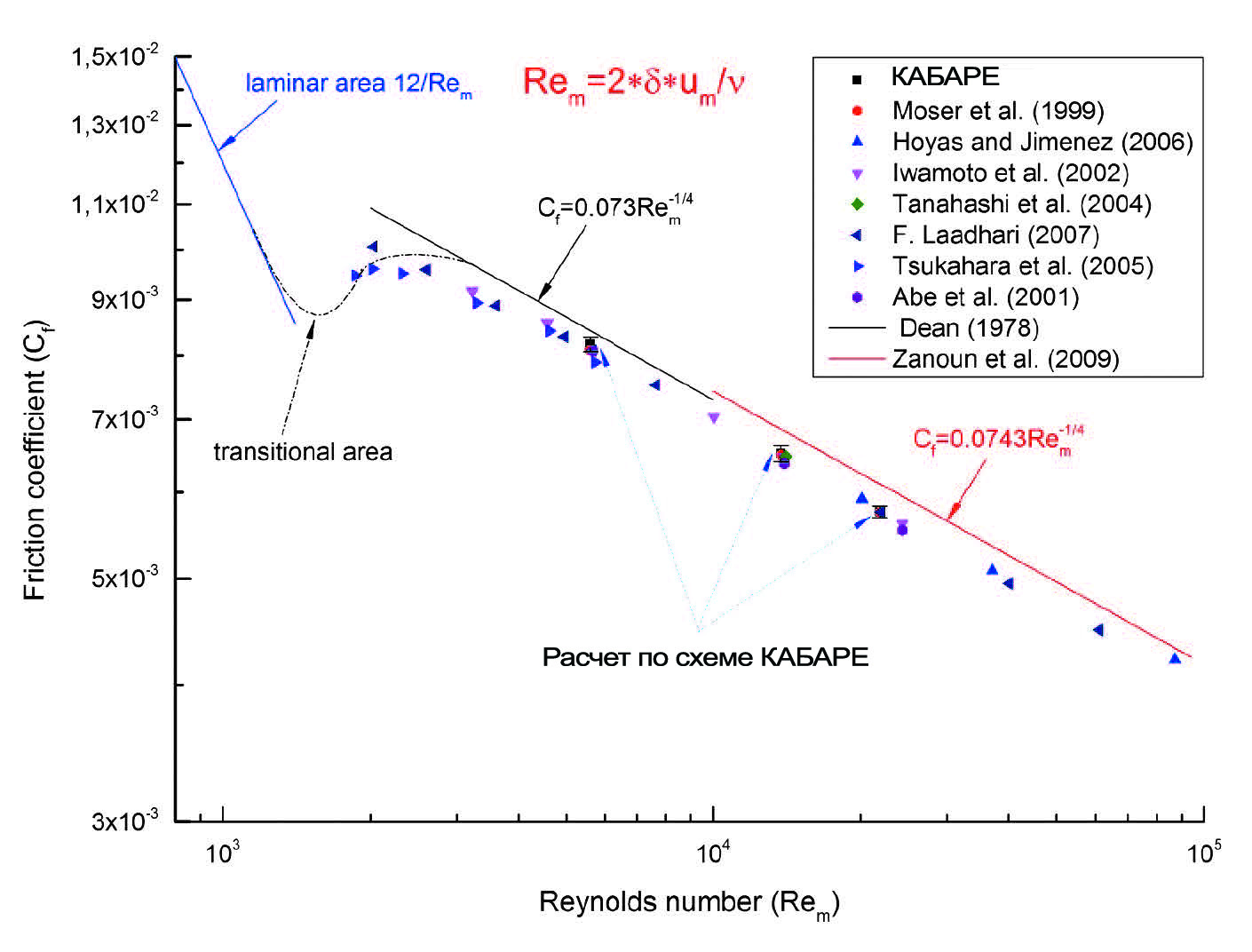
Прямое численное моделирование пристенной турбулентности

© Отдел перспективных исследований и математического моделирования