СТОХАСТИЧЕСКИЕ МАТЕМАТИЧЕСКИЕ МОДЕЛИ РАСПРОСТРАНЕНИЯ РАДИОНУКЛИДОВ В СИЛЬНО НЕОДНОРОДНОЙ ТРЕЩИНОВАТОЙ СРЕДЕ

Одной из первоочередных задач при обосновании безопасности объектов хранения РАО является задача выполнения консервативных оценок рисков, связанных с распространением радиоактивных примесей на большие расстояния. Проведенные в США натурные эксперименты MADE (MacroDispersion Experiment) реального природного масштаба, в которых в естественных условиях исследовалась миграция примеси, инжектированной в водоносный слой, показали, что в неоднородных средах профили концентрации трассера существенно асимметричны. Они имеют сильно вытянутые в сторону течения «хвосты», в которых убывание концентрации примеси не соответствует классическому закону молекулярной диффузии Фике и происходит не по экспоненциальному, а по степенному закону. Такой аномальный характер дисперсии радионуклидов при естественной фильтрации в сильно неоднородных водоносных слоях опасен возможностью их миграции на более значительные расстояния, чем считалось ранее.

Ранее используемые в описании этих экспериментов модели с дробной пространственной производной ограничены одномерным случаем и неприменимы к расчету анизотропных процессов. Для решения этой проблемы в ИБРАЭ РАН предложена концепция применения многомерных стохастических моделей случайных блужданий (FLM, Fractal Levy Motion) к моделированию полетов Леви на основе альфа-устойчивых случайных процессов.

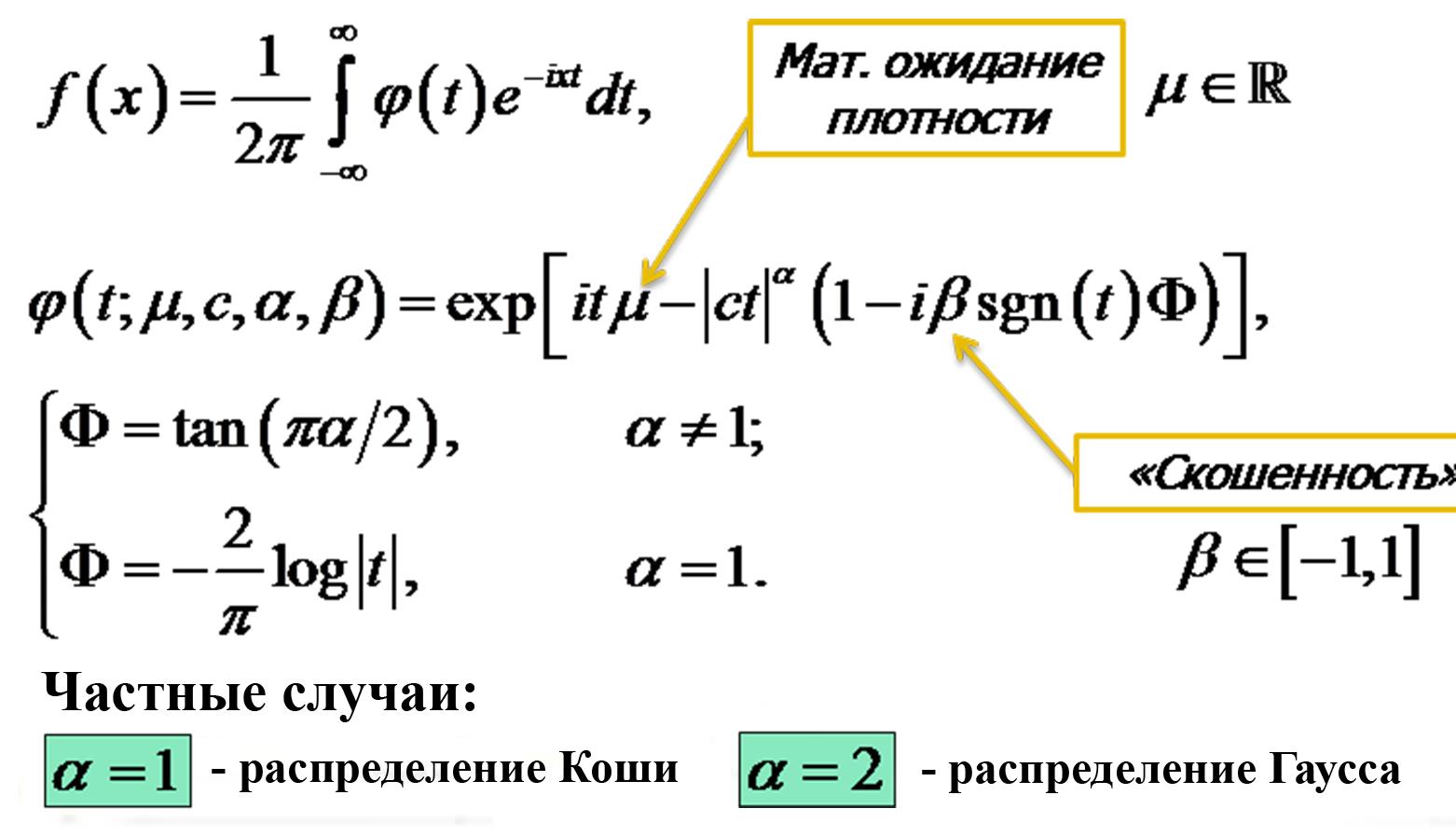
Альфа-устойчивые случайные процессы — это бесконечно делимые процессы, которые являются, в определенном смысле, аттрактором для всех остальных процессов. Они зависят от некоторых параметров, в частности, от параметра a. При a = 2 мы имеем хорошо всем известный гауссов процесс распределения с затухающими по экспоненте хвостами, при a < 2 мы имеем процессы распределения с так называемыми «тяжелыми» хвостами.

Стохастические модели переноса на основе альфа-устойчивого распределения

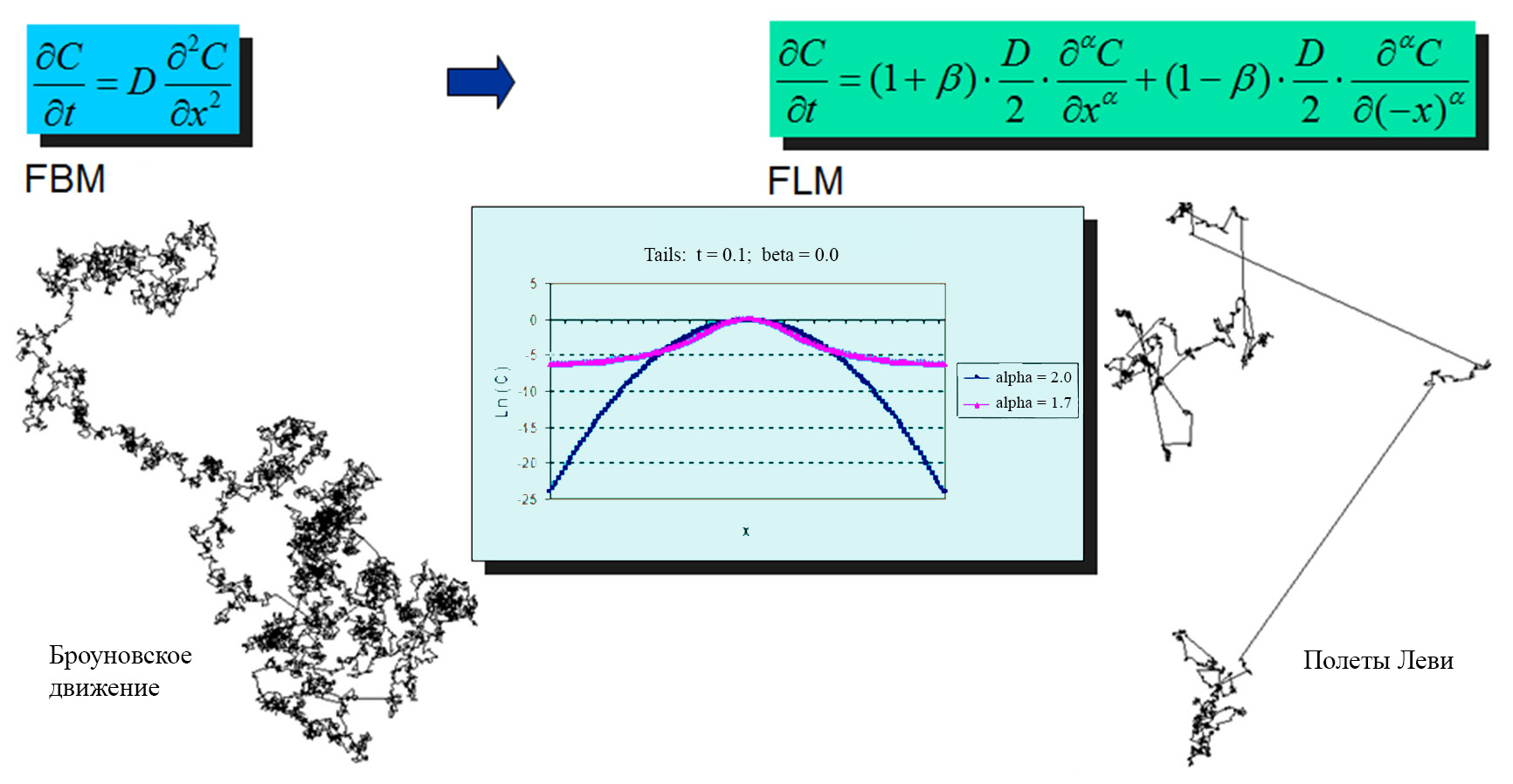
Например, если рассмотреть уравнение Колмогорова в одномерном случае для различных a, то при a = 2 оно сводится к обычному уравнению диффузии с неким коэффициентом, а при 1< a < 2 к так называемым уравнениям диффузии с дробными производными. Если случайный процесс Гаусса описывает случайное блуждание частицы, не совершающей далеких прыжков, то при a ≠ 2 мы имеем иные процессы распределения, так называемые «полеты Леви», которые хорошо подходят для моделирования просачивания загрязнений через трещины в геологических средах.

Переход от модели классической диффузии к неклассической модели диффузии с дробными производными

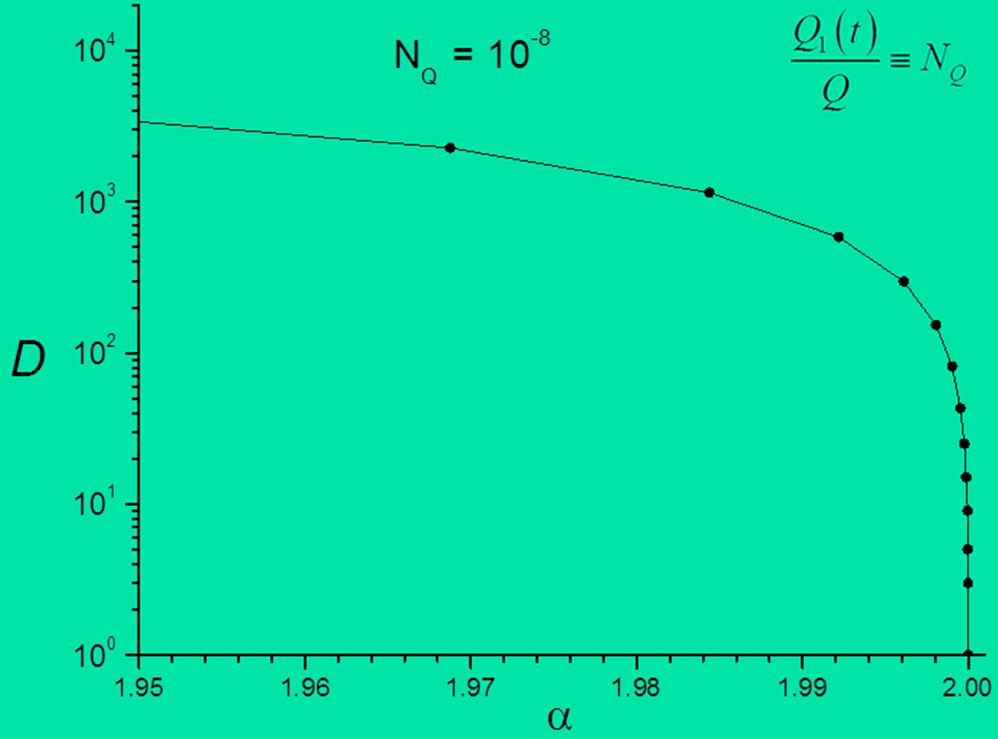
Принципиально важно, каким уравнением описывается процесс распространения загрязнения. Определяющую роль здесь играет величина коэффициента a при операторе дробной производной. В качестве примера можно привести график зависимости эффективного коэффициента диффузии от a. При a = 2 мы имеем классический процесс диффузии, а при меньших значениях a имеет место аномальная диффузия.

Зависимость эффективного коэффициента диффузии от степени дробности производной

По оси ординат на графике отложен эффективный коэффициент диффузии, который был бы у гауссова процесса, если бы мы использовали этот гауссов процесс. При уменьшении значения коэффициента a с 2 до всего лишь до 1.95 эффективный коэффициент диффузии D возрастает на три порядка. Поэтому при оценке надежности захоронений ОЯТ и РАО важны не столько характеристики среды на данный момент времени (за тысячи лет ареография, конечно, изменится), сколько то, как определяется действующий коэффициент диффузии.

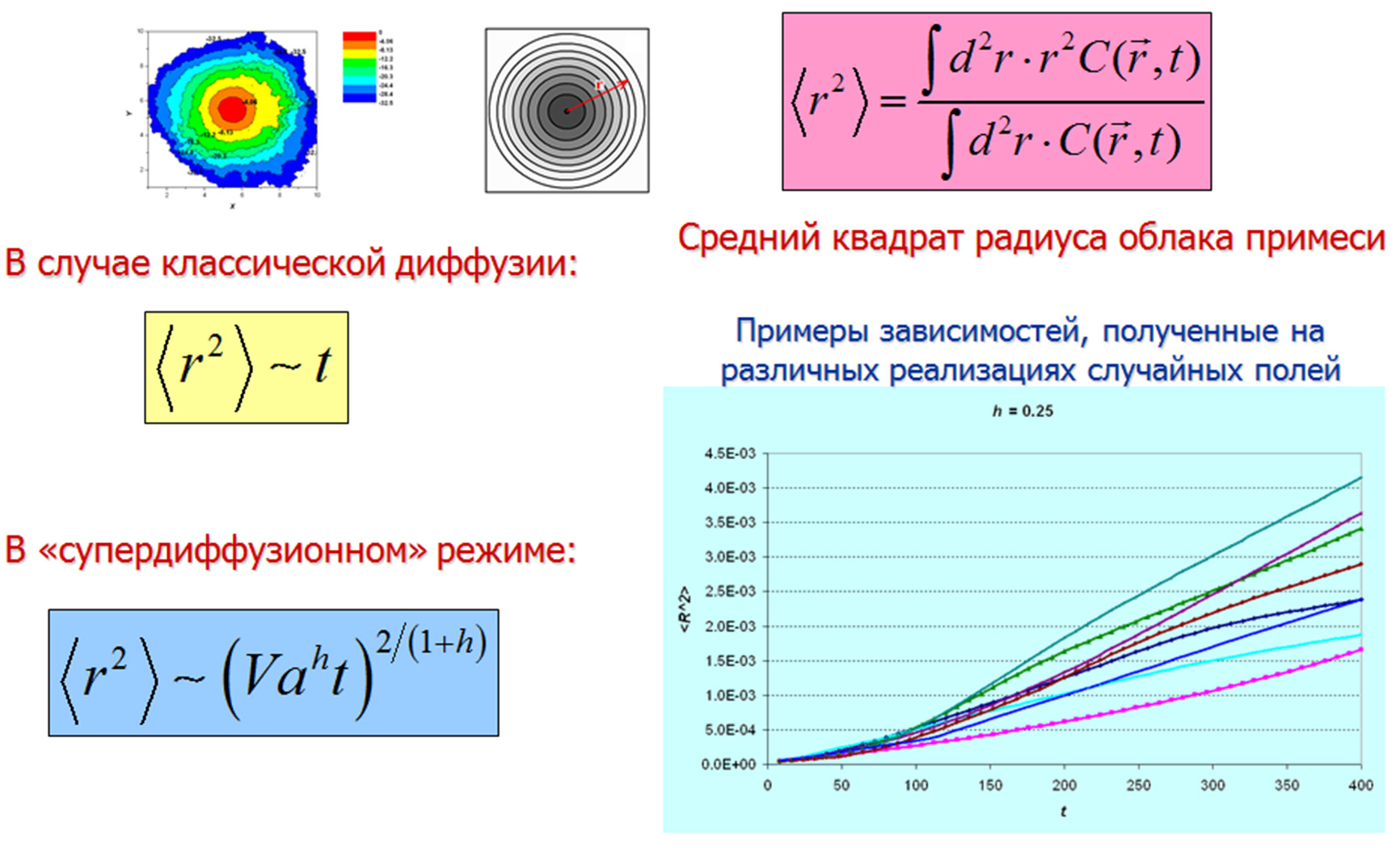
Распространение примеси с течением времени в различных режимах диффузии

Учитывая широкий спектр возможного характера распространения радионуклидов в неоднородных средах, в ИБРАЭ РАН проведены фундаментальные исследования, по итогам которых на основе оригинальных генераторов случайных величин апроксимационного типа разработаны одномерная, двумерная и трехмерная стохастические робастные (устойчивые к внешним воздействиям) модели распространения примеси с «тяжелыми» хвостами функции распределения. Эти модели использовались для описания реальных процессов дисперсии радионуклидов в неоднородных средах (в частности, в экспериментах MADE).

Также разработан ряд моделей, относящихся к другому классу стохастических моделей фрактальных блужданий — Fractal Brownian Motion (FBM) c коррелированными приращениями во времени. Они предназначены для описания результатов, полученных в лабораторных условиях при исследовании процессов аномальной дисперсии (как субдиффузии так и супердиффузии).

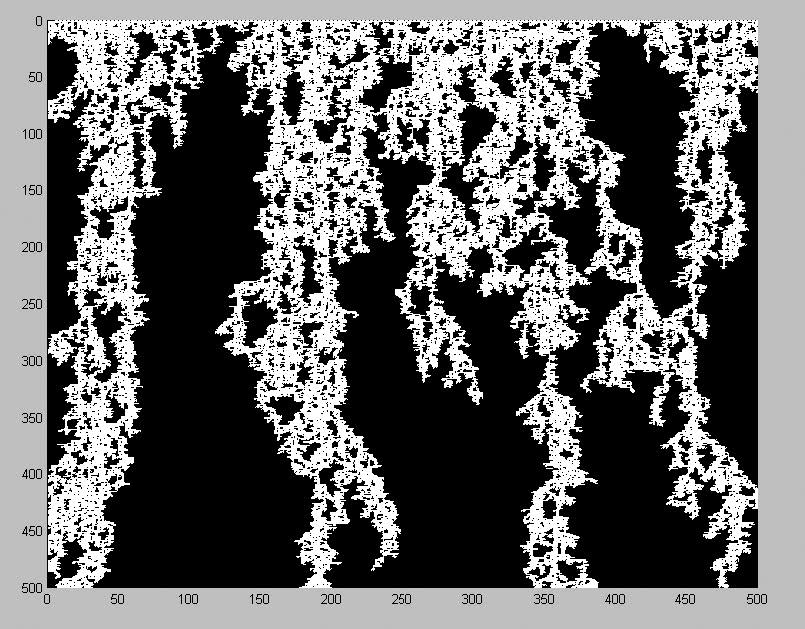
На основе модели двумерной фрактальной случайной трещиноватой среды реализован алгоритм прямого численного моделирования распространения радиоактивного загрязнения, который позволяет строить анизотропные среды в различных направлениях (как по горизонтали, так и по вертикали).

Созданные в ИБРАЭ РАН стохастические модели представляют собой вычислительную основу для разработки программных кодов, предназначенных для расчета и прогнозирования миграции радионуклидов в неоднородных геологических средах и решения задач обеспечения безопасности пунктов долговременного захоронения радиоактивных отходов. Разработаны такие детерминированные модели расчета переноса влаги в сильноконтрастных трещиноватых средах на основе алгоритма КАБАРЕ, которые могут быть использованы в интересах нефтедобывающей промышленности.

Сравнение зависимостей от времени пиковой концентрации (max) и среднего значения (mean) трассера в эксперименте MADE-2 с результатами расчетов по двумерной стохастической модели с «тяжелыми» хвостами функции распределения (сплошные линии)		Просачивание воды в трещиноватой среде. Результаты расчета по схеме КАБАРЕ

© Отдел перспективных исследований и математического моделирования